Benchmark Testing
Testing dBSea’s Solvers in Multiple Comparisons with Well-Known Benchmark Problems
We here present solutions to a range of well-defined underwater sound propagation calculation problems for the comparison of dBSea’s algorithms to the open-source method based on the same modelling approach.
Many of the examples will link to “UWA” files. These are dBSea scenario files that can be viewed in dBSea BASIC (freely available from: http://www.dbsea.co.uk/media/30273/dBSea-Basic-220.zip).
Please note that while ray tracing methods have been included in this document for the sake of completeness, they are generally not suitable for low-frequency problems (wavelength > 1–3% of depth).
1. Upslope Wedge
1.1 ASA Benchmark
The ASA Benchmark problems (Jensen & Ferla, 1989) represent a classic base for comparison of propagation modelling. The UWA file for this scenario is available from: UWA File
Image 1. Schematic of scenario for wedge problem
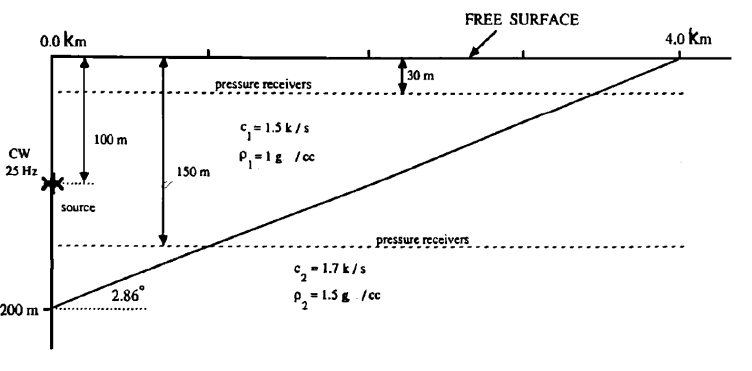
The following results are based on a comparison of dBSea’s solvers with solvers from the AcTUP toolbox (AcTUP Toolbox), covering the three most popular methods of calculating the sound field, namely:
- Parabolic Equation Method – dBSeaPE & RAM
- Normal Modes Method – dBSeaModes & Kraken
- Ray Tracing Method – dBSeaRay & Bellhop
Note that the scenario is modelled for 25 Hz. At this frequency, we do not expect the two ray tracing methods to work well.
1.1.1 Parabolic Equation Method
Image 2. Transmission losses for dBSeaPE and RAM. Depths 30 m and 150 m are shown in chart, while full transects in colour are presented below.
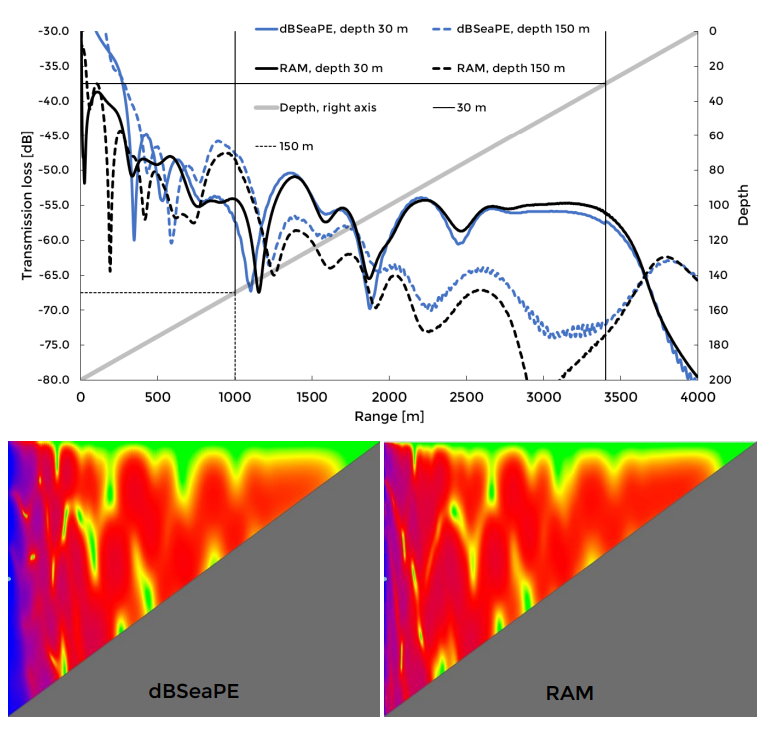
1.1.2 Normal Modes Method
Image 3. Transmission losses for dBSeaModes and Kraken. Depths 30 m and 150 m are shown in chart, while full transects in colour are presented below.
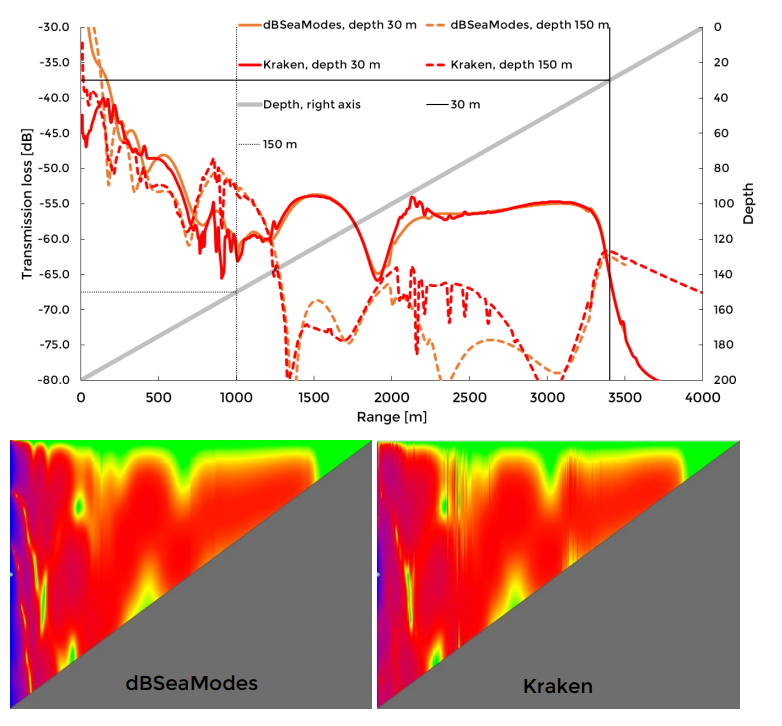
1.1.3 Ray Tracing Method
Image 4. Transmission losses for dBSeaRay and Bellhop. Depths 30 m and 150 m are shown in chart, while full transects in colour (-20 dB to -70 dB) are presented below.
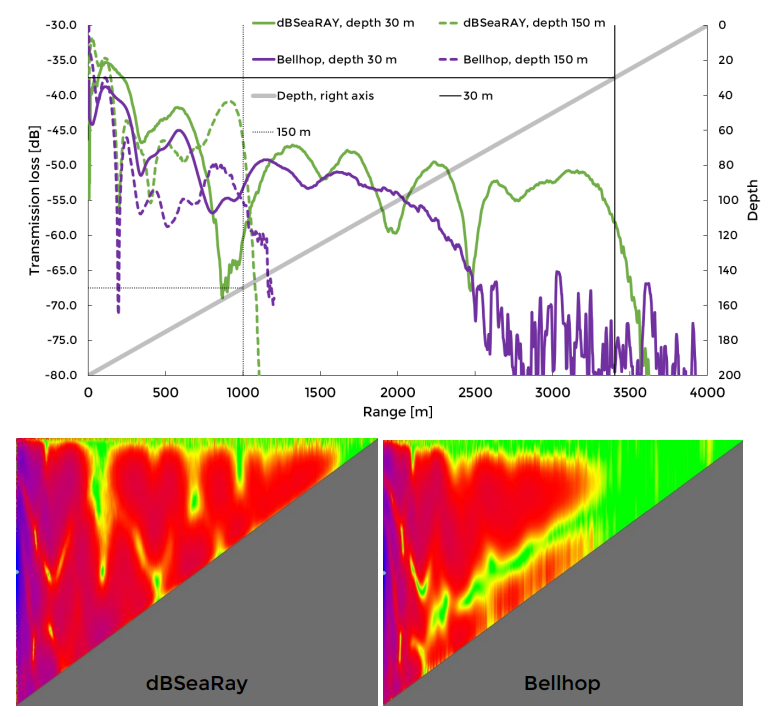
Note that neither of the ray tracing methods penetrate the sediment, and so the receiver depth at 150 m terminates shortly after a range of 1000 m. Notice that dBSeaRay reproduces the results well from both the parabolic equation method and the normal modes method, despite being unsuitable for the chosen frequency (25 Hz).
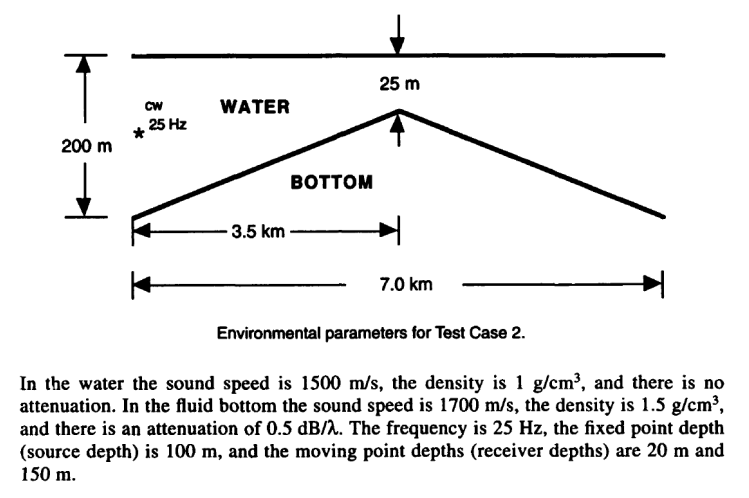
2. Up-Down Energy Conservation Problem
2.1 Parabolic Equation Workshop II 1993 – Case II
An upslope-downslope problem formulated to test the energy conservation in strongly range-dependent environments was formulated in (Chin-Bing et al., 1993). The UWA file for this scenario is available at: UWA File
Image 5. Schematic outlining upslope-downslope problem.
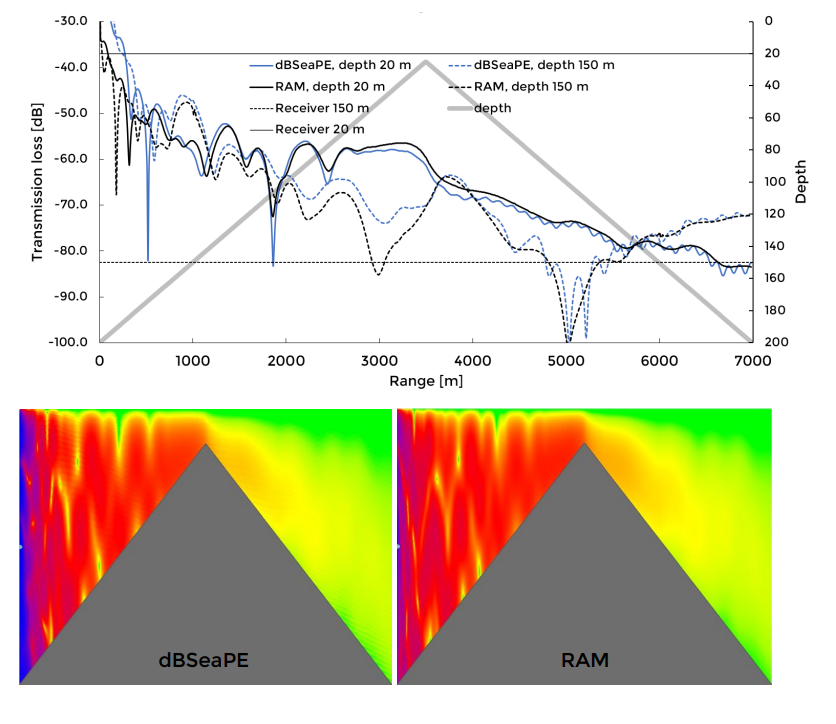
2.1.1 Parabolic Equation Method
Image 6. Transmission losses for dBSeaPE and RAM. Depths 20 m and 150 m are shown in chart, while full transects in colour are presented below.
2.1.2 Normal Modes Method
Image 7. Transmission losses for dBSeaModes and Kraken. Depths 20 m and 150 m are shown in chart, while full transects in colour are presented below.

3. Flat-Bottomed Waveguide
3.1 Pekeris Problem
The Pekeris problem is a horizontally flat waveguide, designed to test propagation in an environment with a moderately absorbent sediment. See here for details about the Pekeris Problem

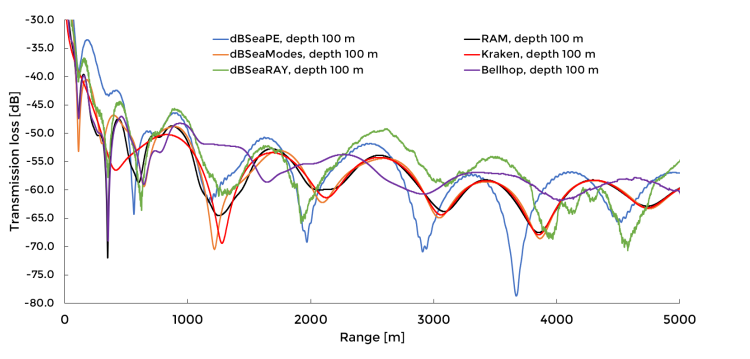
3.1.1 Summary of All Methods
Image 8. Transmission losses for all three methods in the flat waveguide.
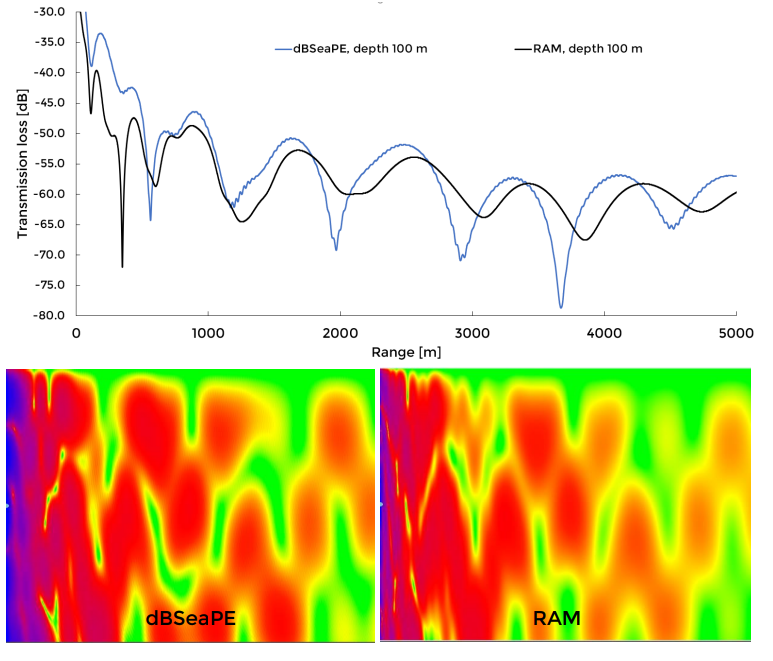
3.1.2 Parabolic Equation Method
Image 9. Transmission losses for dBSeaPE and RAM. Depth 100 m is shown in chart, while full transects in colour are presented below.
3.1.3 Normal Modes Method
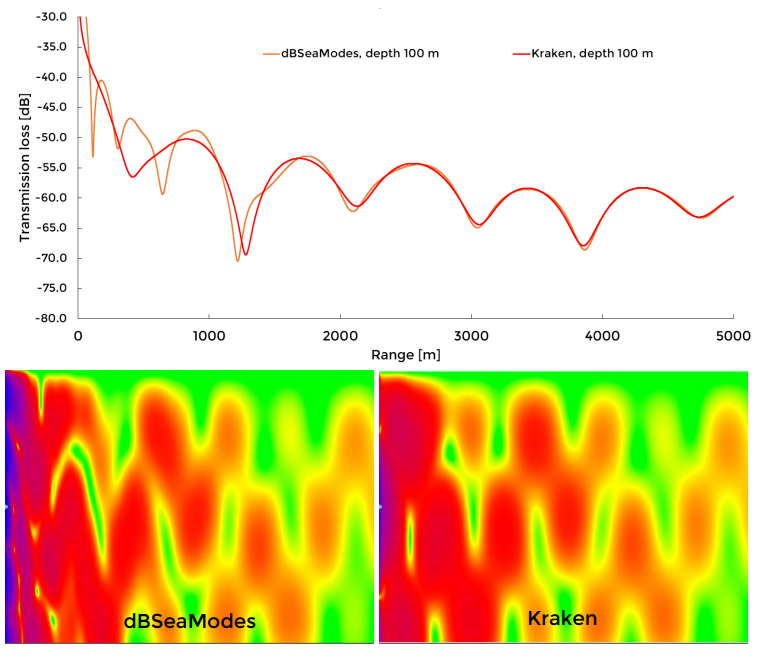
Image 10. Transmission losses for dBSeaModes and Kraken. Depth 100 m is shown in chart, while full transects in colour are presented below.
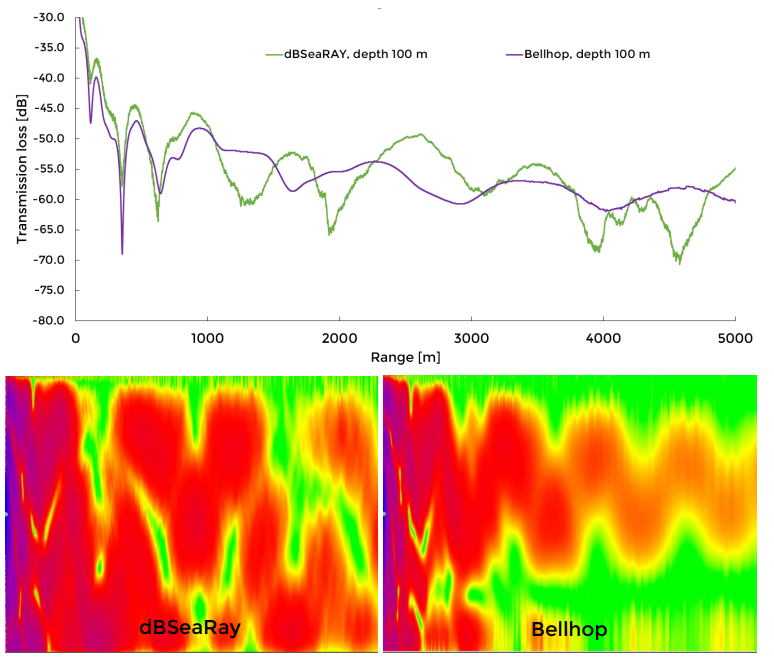
3.1.4 Ray Tracing Method
Image 11. Transmission losses for dBSeaRay and Bellhop. Depth 100 m is shown in chart, while full transects in colour are presented below.
4. References
- Chin-Bing, S. A., King, D. B., Davis, J. A., & Evans, R. B. (1993). PE Workshop II. Stennis: Naval Research Laboratory.
- Jensen, F. B., & Ferla, C. M. (1989). Numerical solutions of range-dependent benchmark problems in ocean acoustics. Journal of the Acoustical Society of America, 4(87).